Wellen in einer rotirenden Kugel

Entstehung von Wellenstrukturen durch Rotation eines fluiden Körpers

Stand 5.1.2025

Zusammenfassung

Im Fluid einer rotierenden Kugel entstehen Wellenstrukturen, deren Ursache die Rotation ist. Diese Wellenstrukturen sind vielfältig und komplex. Ihre Form und Größe ändern sich mit der Drehfrequenz der Kugel.

Die in einer rotierenden Kugel möglichen Wellenlängen und Frequenzen lassen sich bei Kenntnis des Durchmessers der Kugel nach einer einfachen Beziehung - dem Wellengesetz - berechnen. Jede rotierende Kugel hat einen inneren und einen äußeren Wellenraum. Das Wellengesetz bestimmt alle Größen und Vorgänge im Kosmos.

1. Über die Entdeckung der Wellenstrukturen

Im Jahr 1978 wurde ich mit dem Problem der Salzkohle konfrontiert. Salzkohle ist Braunkohle mit einem hohen Gehalt an Natriumsalz. Dieses Salz stört bei der Nutzung von Braunkohle; und man suchte nach einer einfachen Möglichkeit, dieses Salz aus der Kohle zu entfernen. Es war naheliegend eine Extraktion mit Wasser zu versuchen. Das Problem bestand nur noch darin, einen geeigneten Apparat zu finden.

Nach gründlicher Überlegung fand ich, dass der Apparat ein senkrechter Hohlzylinder sein musste, in dem ein drehbarer Zylinder zentrisch angeordnet war. Der Bau erfolgte ohne Erlaubnis von "oben ". Der Test verlief sehr erfolgreich, und die weiteren Arbeiten mit dem Apparat wurden verboten.

Später bekam ich die Aufgabe, einen Reaktor für die Umsetzung von Gasen in Flüssigkeiten zu entwickeln. Damit konnte ich am Drehzylinderapparat weiterarbeiten (Siehe Webseite Mehrphasenapparate). In Drehzylinderapparaten entstehen periodische Strukturen, die Taylor (1) sehr gründlich untersucht und als periodischen Vorgang beschrieben hat. Görtler (2) hat als Ursache die Entstehung der Taylorwirbel aus der Strömung längst einer gekrümmten Wand abgeleitet. Für mich entstand sofort die Frage, welche Auswirkung eine doppelt gekrümmte Wand haben würde; und ich baute im Jahr 1987 eine erste Apparatur mit einer rotierenden Kugel (Bild1)

Bild 1 Apparatur von 1987

Nachdem es mir gelungen war, die Strukturen in der Kugel durch suspendierte Feststoffteilchen oder Einspritzen von Tinte sichtbar zu machen, hatte ich eine große Anzahl schöner Bilder, die ich als Wirbel deuten wollte aber nicht konnte. Ein Besuch meines Geschäftsfreundes Frank Melcher brachte den entscheidenden Denkanstoß. Er sah meine Bilder und sagte :“ Das sind Schwingungen“! Ich antwortete: “Du Holzei, das sind Wirbel“ ! Etwas Anderes passte nicht in mein Denkschema. Nach langem Nachdenken erkannte ich aber, dass ich selber das Holzei war. Die Deutung der Kugelstrukturen als Schwingungen brachte einen wichtigen Fortschritt. Inzwischen habe ich erkannt, dass Wirbel Wellenstrukturen sind.

Bild 2 Verbesserte Apparatur

Nach dem Bau einer neuen Apparatur (Bild 2) konnte die durch den Hals des Kolbens erzeugte Störung vermeiden. Ich verwendete Plastekugeln verschiedener Größe. Es gelangen mir wieder viele interessante Bilder. Auf einigen Bildern waren Strukturen zu erkennen, die man ausmessen konnte. Die Idee von Wellen drängte sich auf. Die Wellenlängen waren drehzahlabhängig und wurden mit steigender Drehzahl kleiner. Das Produkt aus Wellenlänge und Drehfrequenz schien eine konstante Größe zu haben.

Messungen von Erdwellen durch Zürn/Schnidrig (5) bestätigten, dass es sich um Wellen handelt. Ich nannte sie Wellenstrukturen oder rotationsinduzierte Wellen. Es sind Raumstrukturen, deren Größe und Geometrie sich bei bestimmten Drehfrequenzen ändern. Diese Drehfrequenzen nannte ich Umwandlungspunkte. Die Messung dieser Umwandlungspunkte und die damit verbundene Energie hat mich viele Jahre beschäftigt. Dank der Hilfe durch meinen Schulfreund Joachim Bleck ist es mir gelungen, ausreichend genaue Messungen durchzuführen. Die Erkenntnis, dass auch außerhalb der Kugel Wellenstrukturen auftreten, erforderte weitere Versuche.

2 Die ungestörte Kugel

In den bisherigen Arbeiten wurde eine Kugel als ungestört bezeichnet, wenn Abweichungen von der idealen Geometrie, Öffnungen an der Oberfläche sowie innere Einbauten keinen merklichen Einfluss auf die Wellenstruktur in der Kugel haben. Spätere Arbeiten haben gezeigt, das auch eine feste Oberfläche als Störkörper wirkt. Ungestörte Kugeln lassen sich im Versuch nur schwer realisieren.

Die Gasplaneten Saturn und Jupiter haben zwar keine feste Oberfläche, aber einen inneren Störkörper, dem diese Planeten ihr Magnetfeld zu verdanken haben.

Als Umwandlungspunkte bezeichnet man die Drehfrequenzen, bei denen sich die Wellenstrukturen in der Kugel drehzahlbedingt ändern. Die Versuchsapparatur nach Bild 2 wurde für die Beobachtung der Strukturen während der Rotation verwendet.

Alle Bewegungen und Strukturumwandlungen im Fluid einer rotierenden Kugel müssen sich in der Änderung der Antriebsleistung für die Drehung der Kugel bemerkbar machen. Für die Messungen wurde die Kugel in senkrechter Position direkt auf der Motorwelle befestigt. Dadurch konnten einige mechanische Störungen vermieden werden.

Den Verlauf der Antriebsleistung in Abhängigkeit von der Drehfrequenz zeigt Bild 3. Die Strukturänderungen sind durch Peaks in der Kurve (Umwandlungspunkte) deutlich abgebildet.

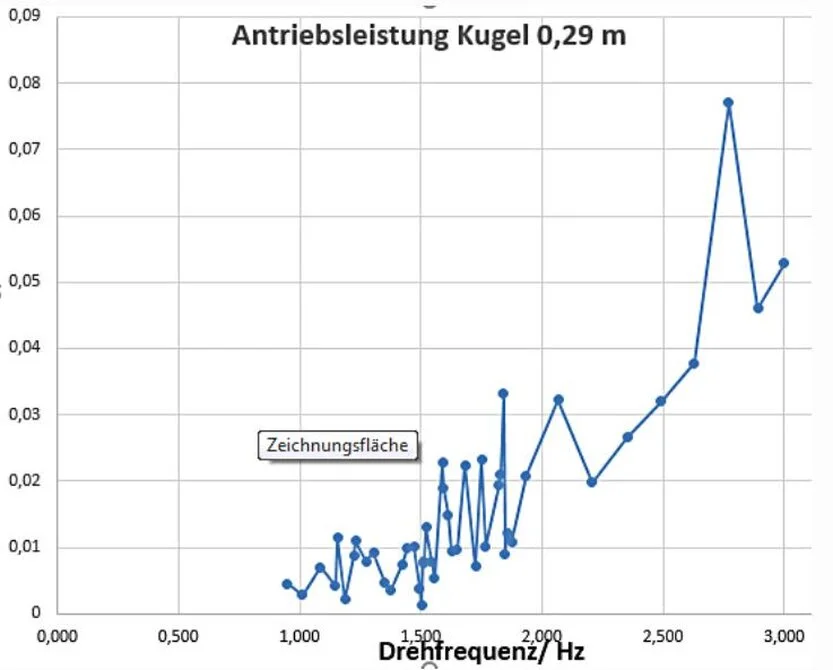
Bild 3 Umwandlunsgpunkte einer luftgefüllten Kugel

Der größte Teil der umfangreichen Messungen erfolgte mit Luft als Medium. Für Wasser wurden gleiche Umwandlungsgpunkte gemessen. Die Messergebnisse für die Umschlagpunkte (Frequenzen) lassen sich in zwei Arten von Zahlenfolgen

einordnen:

1. Eine Hauptfolge p=3^p p=0,1,2,3...p
2. Nebenfolgen f=2v v=0,1,2,3...v Verdoppelungsfolge für die Frequenzen

Der russische Geowissenschaftler W.Piotrowskij (4) hat im letzten Jahrhundert bei der statistischen Analyse der Oberflächenstrukturen der Erde herausgefunden, dass wichtige Maße sich in Zahlenfolgen anordnen lassen, die über den Faktor "3" verbunden sind. Damit ist durch ihn die Hauptfolge entdeckt worden; und sie soll Piotrowskijfolge und ihr Exponent Piotrowskiexponent genannt werden.

Die Wellenlängen, die im Inneren einer rotierenden Kugel (innerer Wellenraum) und in der Umgebung der Kugel (äußerer Wellenraum) mit dem Durchmesser D (bestimmende Größe) möglich sind, erhält aus dem Wellenlängengesetz: (1)

λ=Dx2^-vx3^-pp,v = 0,1,2,3… ℷ= Wellenlänge

ν= v₀x2^-v x3^-3 v= Frequenz

Τ= T₀ x2^-v x3^-p T= Periodenlänge

W=λ x v W = kosmische Wellengeschwindigkeit

Aus den Daten der Erdrotation erhält man W= 0,00315268 m/s. Eine neue Berechnung ergab:

Das Wellenlängengesetz wurde aus Versuchen unter isothermen Bedingungen abgeleitet.

Dieses Gesetz beschreibt alle Größen und Vorgänge im Kosmos, die von Wellenstrukturen bestimmt werden. Die im Kosmos vorkommenden Wellenstrukturen sollen Kosmoswellen genannt werden.

Für Rechnungen mit dem Wellengesetz im Kosmos braucht man einen Wert für "D". Dieser Wert ist nicht bekannt. Um mit dem Wellengesetz zu arbeiten, kann man mit Hilfe einer bekannten, kosmischen Größe ein Wellenlängenschema aufstellen, in dem alle nach de Wellengeesetz erlaubten Werte enthalten sind. Verwendet man für die Größe "D" den Gitterparameter von Silicium, der D= 543,102 0504 (89) pm (Wikipedia), hat man das zur Zeit genaueste Wellenlängenschema. Die Aufstellung des Wellenlängenschemas ist auf der Seite "Wellen im Kosmos" erläutert.

Die in unserem Universum gemessenen Größen aber auch die Größe des Elektrons passen exakt in ein gemeinsames Wellenlängenschema.

Für eine Einheitskugel D=1 ergibt sich alsWellenlängenschema (Tabelle 1)

Tabelle 1

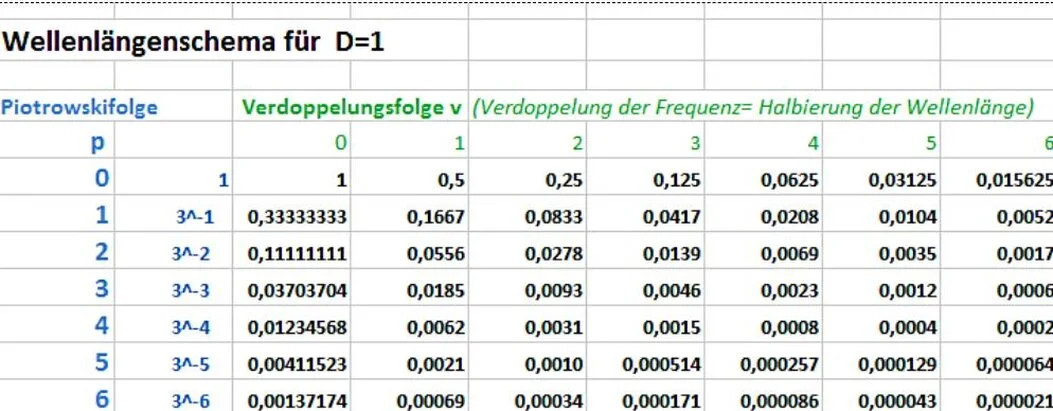
Das Wellenlängenschema einer beliebigen Kugel erhält man durch Multiplikation der Werte aus obiger Tabelle mit dem Durchmesser der Kugel.

Der Beginn von Haupt- und Nebenfolge ist bei allen Kugeln die Drehfrequenz f*. Diese Größe soll Grundfrequenz heißen. Die zugehörige Wellenlänge ist der Kugeldurchmesser. Umwandlungsgpunkte werden erreicht, wenn sich die Drehfrequenz um das Doppelte oder das Dreifache von einer in der Kugel vorhandenen Frequenzen erhöht oder vermindert. Beim Umwandlungsvorgang entstehen neue Strukturen, deren Wellenlängen bei Änderung um den Faktor 2 oder 3 kleiner oder größer sind.

Beim Umwandlungsvorgang werden vorhandene Strukturen in der Regel umgeformt. Einige Strukturen bleiben aber über einen großen Bereich der Drehfrequenz erhalten.

Das Innere einer rotierenden Kugel ist mit Wellenstrukturen ausgefüllt. Die Gesamtheit aller Strukturen bildet den inneren Wellenraum.

Auch außerhalb der Kugel gibt es Wellenstrukturen - den äußeren Wellenraum.

Beide Wellenräume sind eine Einheit, auch wenn sie bei der Versuchskugel oder beim Erdkörper durch eine feste Oberfläche getrennt sind.

Die bei den meisten Versuchen verwendete Kugel hatte einen inneren Durchmesser von 196 mm, welcher zufällig im kosmischen Wellenlängenschema zu finden ist. Damit ist zu erklären, warum die in der Laborkugel beobachteten Wellenstrukturen den Wellenstrukturen auf der Oberfläche der Planeten sehr ähnlich sind.

Die Wellenstrukturen, die in und um Kugeln entstehen und deren Durchmesser im kosmischen Wellenlängenschema nicht vorkommen, haben andere Wellenstrukturen. Das konnte in Versuchen bestätigt werden.

Das Frequenzschema erhält man, indem man die die Ausbreitungsgeschwindigkeit der Wellen (W) durch die Werte des Wellenlängenschemas dividiert. Für kosmische Frequenzen ist die Aufstellung eines Frequenzschemas auch auf der Basis des Cäsium Standards möglich. Eine der am genauesten, gemessenen Frequenzen ist eine Schwingung des Cäsiumatoms:

hyperfine transition frequency of Cs-133 = 9192631770 Hz. (NIST Standard Reference Database 121)

3. Messung der Umwandlungsenergie

Der Umwanlungsgvorgang lässt sich in einer wassergefüllten Kugel gut beobachten. Er dauert im Versuch mit Wasser 3 bis 10 Minuten. Bei Versuchen mit Luft wurden Umschlagzeiten zwischen 7 und 20 Sekunden gemessen.

Für die Messungen wurde ein Gleichstrommotor verwendet. Kurz vor Erreichen des Umwandlungspunktes wurde die Motorspannung um einen solchen Betrag erhöht, das der Umschlag einsetzte. Aus dem Stromverlauf (Bild 4) und der Spannung wurde die Umwandlungsenergie berechnet.

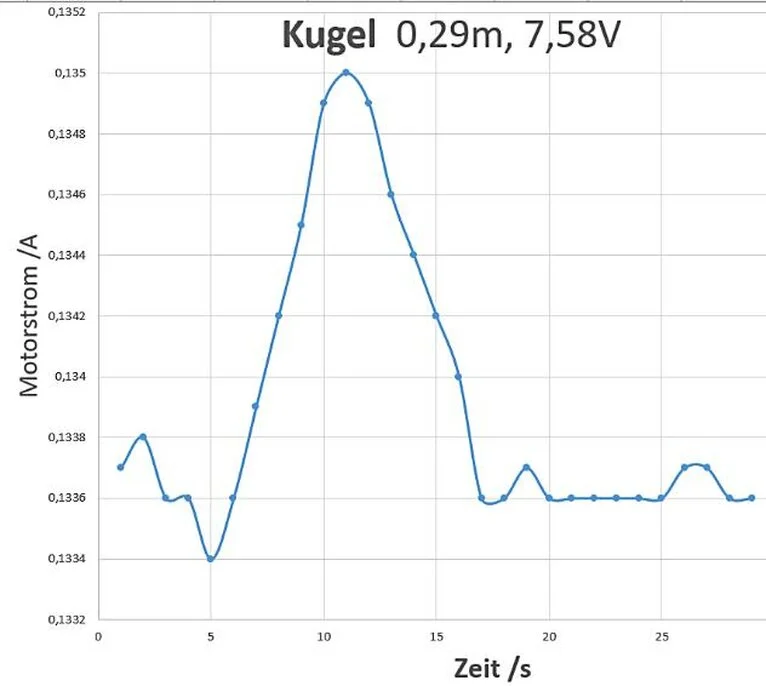
Bild 4 Stromverlauf beim Umwandlungsvorgang

Bild 4 zeigt den zeitlichen Verlauf des Umschlagvorgangs. Der Verlauf der Kurve ist typisch für alle Messungen. Wenn alle Strukturen in der Kugel einen diskreten Wert für für Wellenlänge haben, müsste die Kurve einem Dirac-Peak ähnlich sein. Der Kurvenverlauf deutet auf eine Streuung der Werte hin.

Die Kurven des Stromverlaufs bei Steigerung und Verminderung der Drehfrequenz sind sehr ähnlich aber mit umgekehrten Vorzeichen (Bild 5). Die Energie, die dem System bei der Erhöhung der Drehfrequenz zugeführt wird, wird bei der Verminderung der Drehfrequenz wieder frei und vermindert die für den Motor notwendige Antriebsleistung .

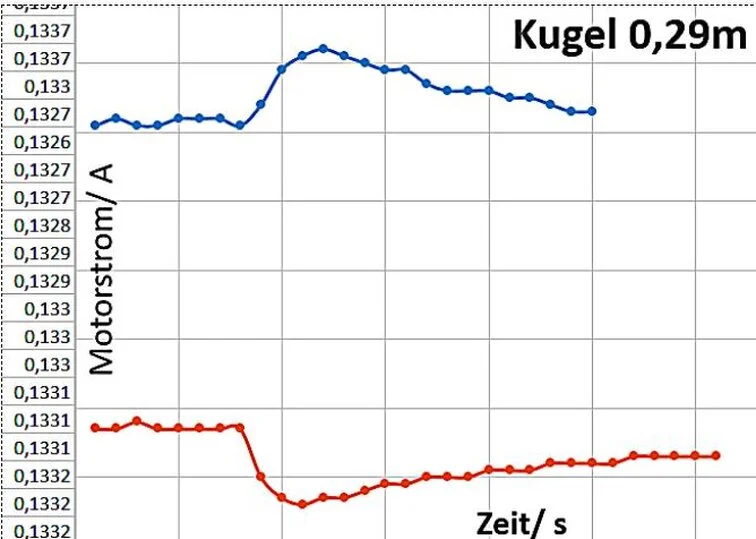
Bild 5 Stromverlauf beim Umwandlungsvorgang

obere Kurve: Erhöhung der Drehfrequenz

untere Kurve: Verminderung der Drehfrequenz

Die Umwandlungsenergie nimmt mit der Drehfrequenz zu (Bild 6.1)

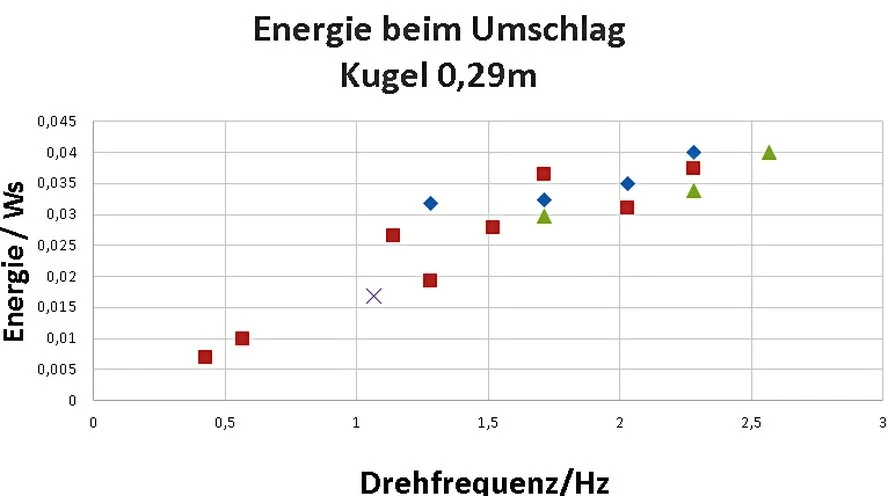
Bild 6.1 Umwandlungsenergie in Abhängigkeit von der Drehfrequenz

Trägt man das Verhältnis aus Umwandlungsenergie und Drehfrequenz (W/f) in einem Diagramm über dem Durchmesser auf, erhält man eine Gerade ( Bild 6.2).

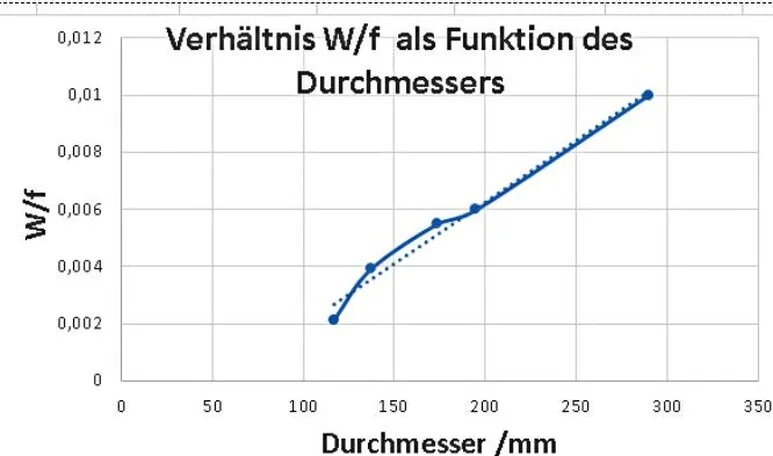
Bild 6.2 Verhältnis W/f als Funktion des Durchmessers

Aus diesem Zusammenhang ergibt sich für dieUmwandlungsenergie nach einer einfachen empirischen Beziehung :

E(Umschlag)=k*f*D

k= 3,2E-05 /Ns²

f= Drehfrequenz /Hz

D= Durchmesser der Kugel /m

Diese empirische Gleichung wurde aus Versuchsergebnissen mit Kugeln von 0,1 ...0,29 m erhalten. Der Faktor "k" ist in diesem Bereich eine Konstante. Es ist aber nicht auszuschließen, dass "k" bei größeren Kugeln eine Funktion ist.

Wenn ein kosmisches Objekt expandiert , kann bei der Veränderung des Durchmessers ein Umwandlungsgpunkt erreicht werden. Die Umwandlungsenergie wird benötigt, damit die Umwandlung stattfinden kann. Sie ist ein Erfordernis, das die Stabilität rotierender fluider Systeme sichert. Die Umwandlungsenergie muss bei der Berechnung von Expansion und Kontraktion im Universum berücksichtigt werden. Weil sie nicht bekannt ist, ist sie ein Teil der dunklen Energie.

Während des Umwandlungsvorgangs kann man häufig Wellenelemente unterschiedlicher Größe nebeneinander finden (Bild 7). Demzufolge unterliegen Größen von Wellenlängen und Frequenzen einer Streuung. Das bestätigen Messungen von Oberflächenstrukturen der Erde (Gebirge, Dünen, Strandrippel). Eine Streuung der Wellenlänge ist auch aus den Messungen der Umwandlungsenergie (Bild 4) abzuleiten. Die Kurve ist ähnlich einer Gaußverteilung und zeigt den Umschlagvorgang, der in der gesamten Kugel stattfindet. Die Messpunkte streuen um Wert des Umwandlungspunktes . Eine quantitative Beziehung über die Größe des Streubereiches könnte aus Messungen der Oberflächenstrukturen der Erdkugel ermittelt werden.

Bild 6 zeigt sinusförmige Wellenelemente, die unterschiedliche Wellenlängen haben. Diese Wellenelemente sind Teil einer Zylinderstruktur, die sich bei n=3/min gebildet hat. Ein Teil hat die zweite Verdoppelung Drehzahl 12/min) mitgemacht, während der andere Teil (Drehzahl 6/min) verblieben ist und noch die doppelte Wellenlänge hat.

Bild 7 Unterschiedliche Wellenlängen in einer Struktur

oberen Rand, Drehzahl 12,2/min.
die Hauptstrukturen sind Elfen

Auf Bild 7 ist der zeitliche Verlauf einer Strukturänderung (wassergefüllte Kugel) zu sehen. Der gesamte Vorgang dauerte mehr als drei Minuten. Es ist zu erkennen, dass die Änderungen den gesamten Teil der unteren Kugelhälfte umfassen.

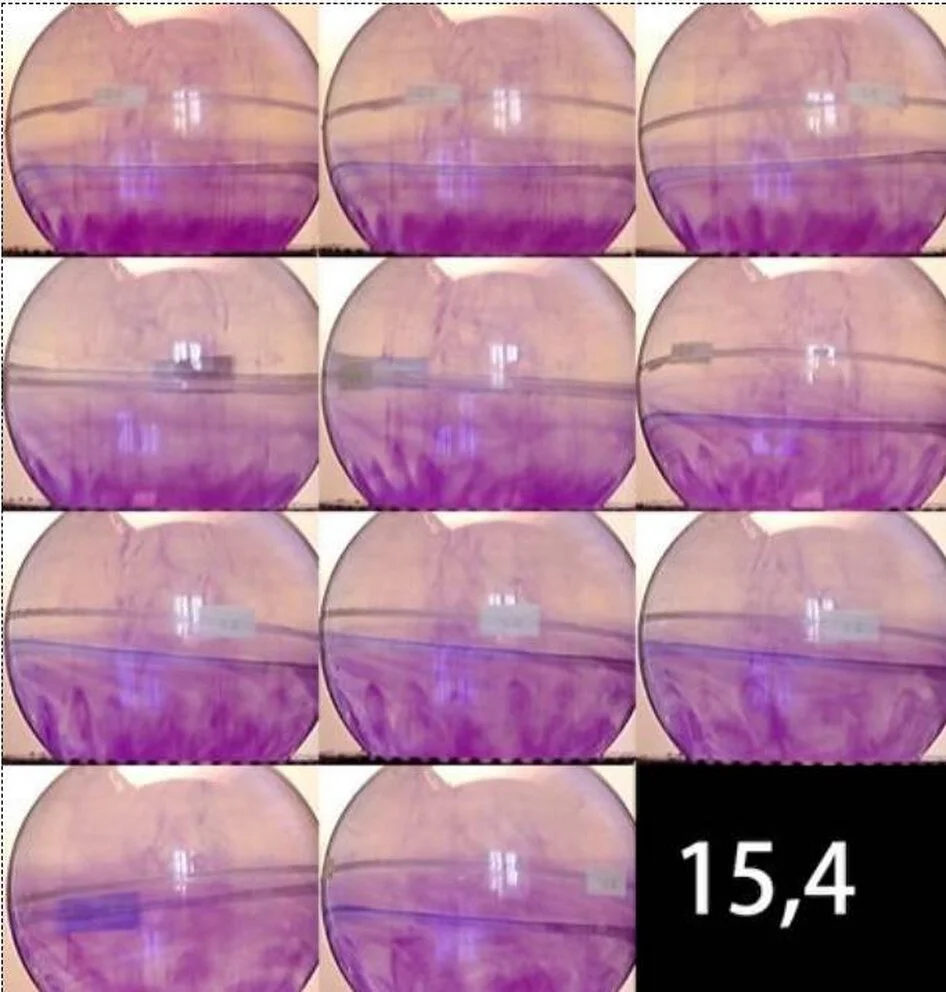
Bild 8 Umschlag bei 15,4/min

4. Strukturen bei verschiedenen Drehzahlen

Die folgenden Bilder wurden aus unterschiedlichen Versuchsreihen zusammengestellt. Sie wurden durch Einspritzen von Tinte und anschließender Veränderung der Drehzahl erzeugt. Diese Methode ist sehr einfach, hat aber Nachteile:

Es können niemals alle Strukturen gleichzeitig dargestellt werden.
Sie ist nur begrenzt reproduzierbar, weil es schwierig ist, beim Einspritzen immer die gewünschte Position zu erreichen.

Man erhält beim Herauf - und Herabregeln der Drehzahl unterschiedliche Strukturen. Beim Einspritzvorgang werden die Strukturen sehr schnell sichtbar.. Die Strukturen sind zusammenhängende, räumliche Gebilde. Sie haben messbare Wellenlängen. Sinusartige Strukturen sind an den Rändern häufig.

Die Kugelstrukturen lassen sich in drei Bereiche einteilen (Bild 7):

* Zylindrische Hauptstrukturen

* Polstrukturen

* Äquatorstrukturen

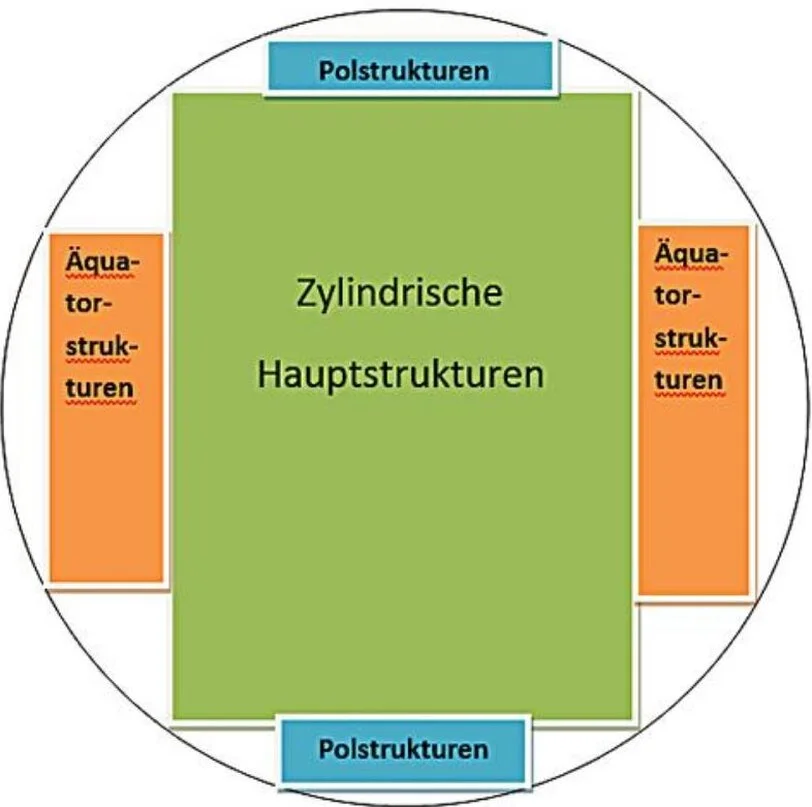
Bild 8 Hauptstrukturen in einer Kugel

Bild 9 zeigt einige Strukturen im Bereich geringer Drehfrequenzen. Derartig komplizierte Strukturen wurden bei diesen Drehfrequenzen nicht erwartet, denn die Grundfrequenz für die 196mm-Kugel bezrägt 1,1/min. Sie sind experimentell noch nicht untersucht.

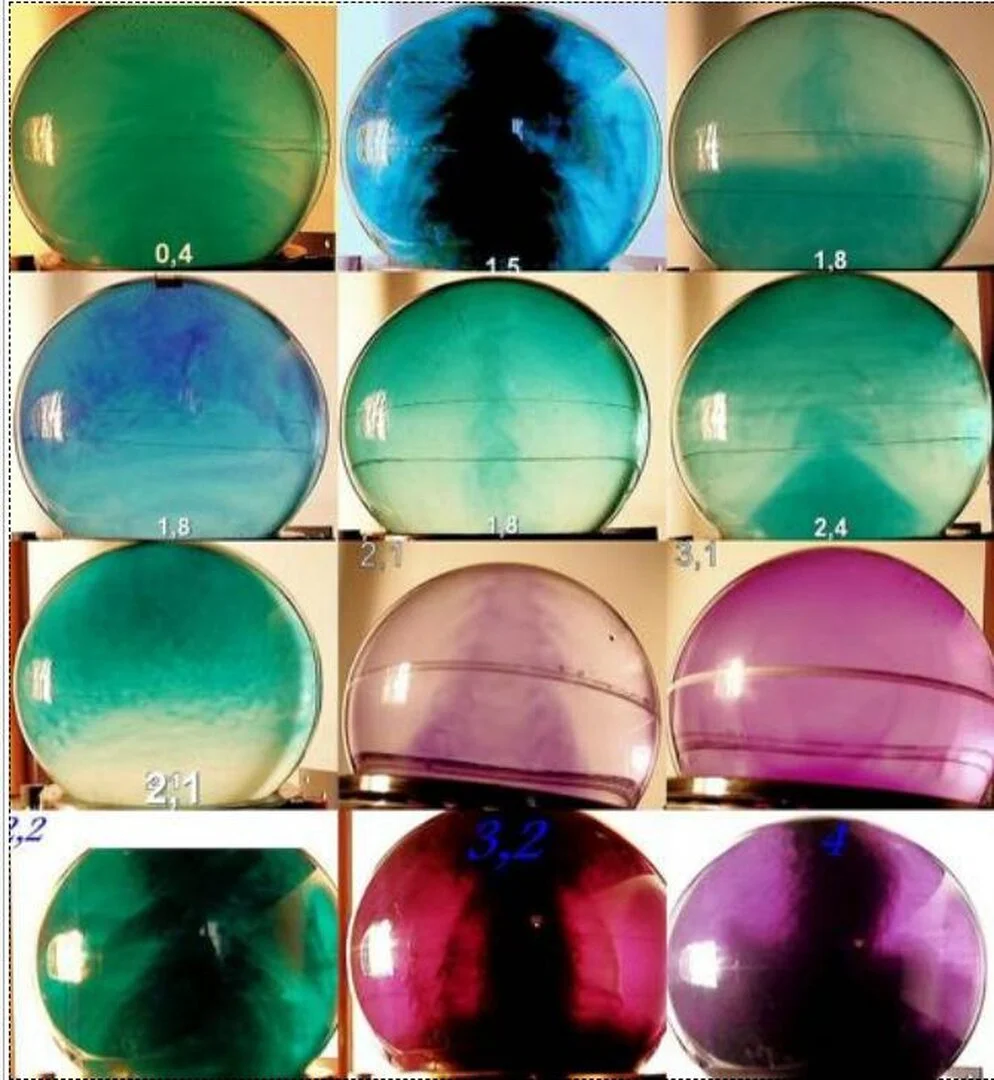
Bild 9 Strukturen bei geringer Drehzahl (Die Zahlenangaben sind Drehzahlen/min)

Zylinderstrukturen treten in der 196-mm-Kugel bei Drehzahlen über 3/min auf. Sie sind bis zu hohen Drehzahlen vorhanden und die Verdoppelungsfolge für die Drehzahl 3/min.

Bild 10 Zylinderstrukturen bei verschiedenen Drehzahlen

Bild 11 Änderung von Zylinderstrukturen bei Verminderung der Drehfrequenz

Bei Verminderung der Drehfrequenz erhält man nicht die gleichen Strukturen, die vor der Drehzahlerhöhung vorhanden waren (Bild 11).

Bild 12 Kugel 196 mm, Drehfrequenz 20/min

Die meisten Bilder zeigen die Zylinder als durchgehende Linien in beiden Kugelhälften. Bild 11 zeigt Zylinder mit Unterstrukturen. Es gibt 9 Ebenen parallel zum Äquator. Parallel zur Drehachse findet man 18 Strukturen.

Alle diese Unterstrukturen gehören einer gemeinsamen Struktur an. Sie sind miteinander verbunden, denn sie wurden durch einen einzigen Einspritzvorgang sichtbar gemacht wobei die einzelnen Ebenen nacheinander sichtbar werden, Bei höheren Drehzahlen gibt es mehrere getrennte Zylinderstrukturen.

Bild 13 Feine Zylinderstrukturen im äquatorialen Bereich

Die Zylinderstrukturen füllen auch den äquatorialen Bereich aus. Die äquatorialen Zylinderstrukturen sind aber bei einer Drehzahl über 50/min nicht mehr zu sehen.

Mit steigender Drehzahl werden die Zylinderstrukturen zahlreicher und feiner. Sie bleiben auch bei hohen Drehzahlen und in großen Maßstab erhalten, wie die Oberflächenbilder der Planeten zeigen.

Bis zu Drehzahlen von etwa 80/min findet man in der 196-mm-Kugel Strukturen, die ich wegen Ihres schönen Aussehens Elfen genannt habe. Sie befinden sich zwischen den Zylinderstrukturen und beginnen immer in der unteren Kugelhälfte. Beide Strukturen wurden bisher niemals gleichzeitig beobachtet. Vermutlich bilden sie das Innere der Zylinderstrukturen ab. Die Elfen sind zart, schön, geheimnisvoll und wurden bisher nur in Kugel ohne Störkörper gefunden.

Bild 14 Elfen bei verschiedenen Drehzahlen, Kugel 196mm

Bild 15 Gegenstruktur für Elfen (Der Polbereich ist leider nicht scharf abgebildet)

Bild 16 Äquatorstrukturen (Kugeldurchmesser 290 mm)

Äquatorstrukturen sind vielfältig, kompliziert und stark abhängig von der Drehfrequenz. Sie sind auch auf der Erdoberfläche zu finden und aber nicht bei den Gasplaneten. Offensichtlich sind sie eine Folge der festen Oberfläche. Die feste Oberfläche hat die Wirkung eines Störkörpers, der einen Störbereich mit senkrechten Strukturen erzeugt. (Siehe Punkt 6)

5. Das Problem " oben und unten" - die Asymmetrie

Bei allen Versuchen unterscheiden sich die Strukturen in beiden Kugelhälften wesentlich. Besonders deutlich zeigt es sich bei den Strukturen bei geringen Drehzahlen / Bild (9) und bei den als Elfen bezeichneten Strukturen (Bild 14).

Wenn auch die Strukturen einzelner Wellenelemente sich sehr ähnlich sind, unterscheiden sie sich in Größe und Form häufig sehr deutlich.

Unterschiedliche Kugelhälften wurden auch bei den Versuchen mit der gestörten Kugel (Punkt 6) festgestellt.

Ein solcher Unterschied ist auch bei den Planeten Jupiter und Saturn (3) sowie bei der Erde und Venus zu finden.

Auch bei den äußeren Wellenräumen gibt es zwei unterschiedliche Hälften; wie erste Versuche zeigen (siehe"Wellen im Kosmos ").

Die Asymmetrie der Wellenräume ist eine grundlegende Eigenschaft rotierender fluider Systeme.
Das Wellenlängengesetz legt für alle Bestandteile eines Wellenraumes diskrete Werte für die Wellenlänge, Frequenz und die Periode fest. Beim Ausmessen von Oberflächenstrukturen auf der Erde (sehr gut möglich bei Google Earth) findet man eine breite Streuung der Ergebnisse. Eine gute Übereinstimmung zum Wellenlängengesetz erhält man nur über eine Durchschnittsbildung mit mehreren Messwerten. Gleiches gilt auch für die Oberflächenstrukturen von Saturn und Jupiter (3).

In einem idealen Wellenraum gibt es keine Abweichungen vom Wellenlängengesetz. In realen Wellenräumen streuen alle Werte um die Werte , die das Wellenlängengesetz bestimmt.. Diese Streuung der Wellenlängen ist eine weitere Eigenschaft des realen Wellenraumes. Streuung und Asymmetrie sind bei allen realen Wellenräumen zu finden.

Bei den Zylinderstrukturen sind die die obere und der untere Hälfte der Kugel verbunden ( Bilder 12, 13)

6. Stofftransport und Reibung in Wellenstrukturen

Die Wellenstrukturen sind Hohlkörper mit scheinbar festen Wänden. Das sieht man sehr deutlich beim Einspritzen von Farblösung in die Kugel. Die Farbe verteilt sich innerhalb oder außerhalb der getroffenen Struktur und bildet diese sehr scharf ab. Bei Verformung der Strukturen infolge Drehzahländerung bleiben die Wände intakt, denn eine Vermischung des Farbstoffes in der Flüssigkeit unterbleibt immer (ausgenommen die unvermeidliche Diffusion).

Beim Einspritzen der Farblösung kann man beobachten, dass sie durch Strömungen transportiert wird, die sich innerhalb und außerhalb der Strukturen auf geschlossenen Bahnen bewegen. Diese Strömungen sind die Bewegung der Welle und bewegen sich mit der Wellengeschwindigkeit W=0,00325 m/s. Wellen und Strömungen treten gemeinsam auf.

Reibung zwischen den Wellenstrukturen gibt es offensichtlich nicht. Würde es sie geben, wären Scherspannungen unvermeidlich, die die Strukturen zerstören würden. Die ausgeprägte Stabilität der Strukturen ist ein Beweis dafür, dass sie sich reibungsfrei gegen einander bewegen. Das Fehlen von Reibung bedeutet, dass für die Existenz der Wellenstrukturen und für die in den Strukturen beobachteten Strömungen keine Energie erforderlich ist. Das ist wichtig, weil in die Wellenstrukturen, die es in den meisten Himmelskörpern gibt, stabil sind.

Ein weiterer Beweis für das Fehlen von Reibung ist die differentielle Rotation, bei der innere und äußere Bereiche der Kugel unterschiedliche Drehfrequenzen und Drehrichtung haben.

Die differentielle Rotation konnte im Versuchsbetrieb mehrmals beobachtet werden. Eine quantitative Auswertung ist aber nicht gelungen.

Die differentielle Rotation ist beim Jupiter sind beim Saturn zu sehen. Dazu hat die NASA (3) einige Videos veröffentlicht.

Bei Kugeln mit einer festen Oberfläche entsteht Reibung, wo die Bewegung der Strukturen (Richtung und Betrag) nicht mit der Bewegung der Kugeloberfläche übereinstimmt. Ebenso ist mit Reibung zu rechnen, wenn in der Kugel Störkörper vorhanden sind. (Störkörper siehe Punkt 6)

7. Kugeln mit einem inneren Störkörper

Bei den Versuchen wurden als innere Störkörper Kugel oder Zylinder verwendet. Man findet einen Störbereich,einen nicht gestörten Bereich und einen Übergangsbereich, in dem Drehstrukturen zu finden sind.

Im ungestörten Bereich gelten die Gesetze der ungestörten Kugel.
Für zylindrische und kugelförmige Störkörper wurde keine wesentlichen Unterschiede gefunden.

Der Störkörper ist eine Kugel:

Der Störkörper erzeugt einen gestörten Bereich, der seinem Durchmesser entspricht. Zwischen dem gestörten Bereich und dem ungestörten befindet sich ein Übergangsbereich, in dem Drehstrukturen zu beobachten sind. Innerhalb der Drehstrukturen besteht eine Wirbelströmung, die für die Entstehung der Magnetfelder der Planeten von Bedeutung ist.

Bild 16 Kugel 196 mm, Störkörper 40 mm

In der Übergangszone entstehen zylindrische Längsstrukturen, die typisch sind für die gestörte Kugel. Dazu auch Bild 19.

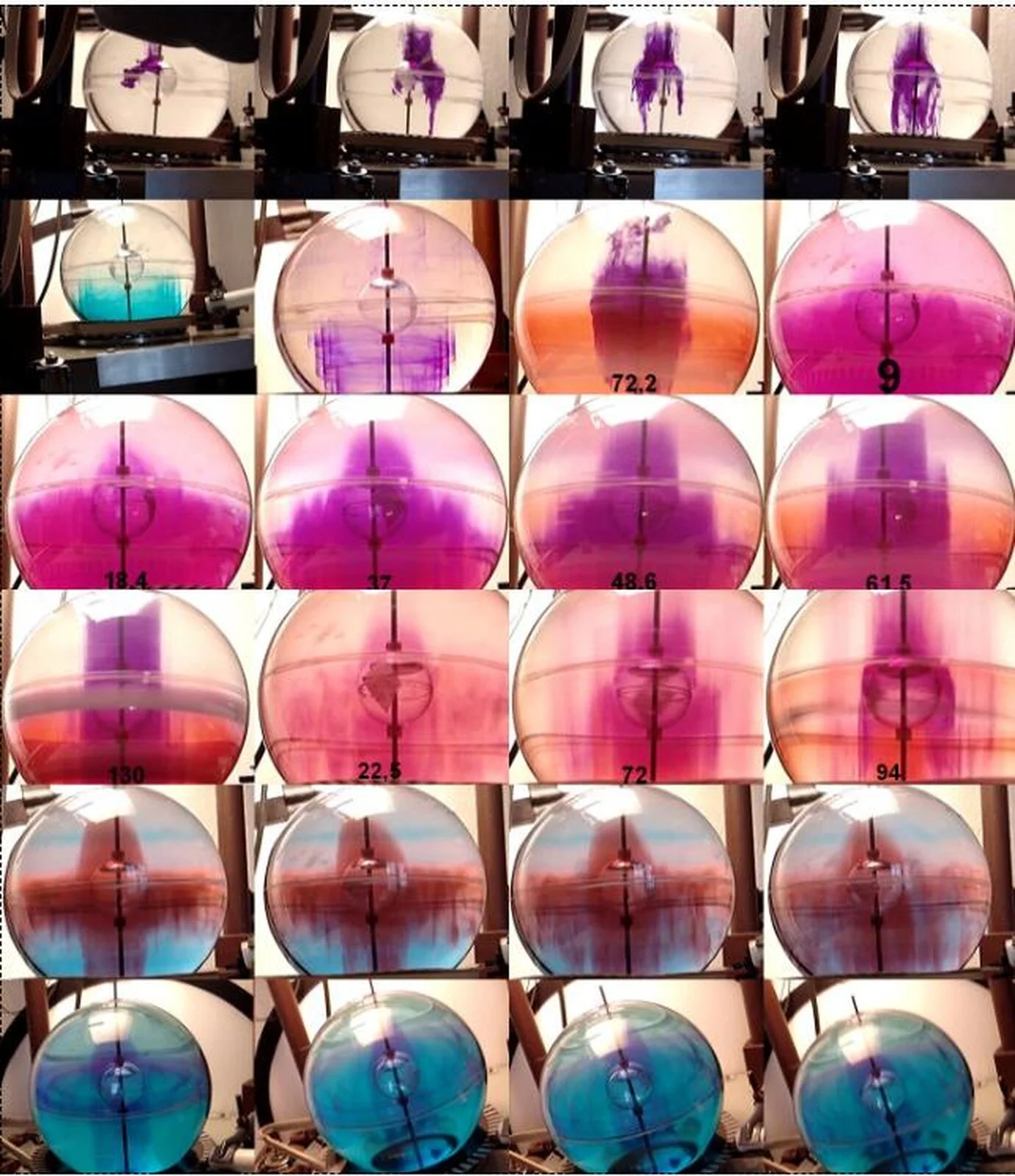
Bild 17 Kugel 196 mm, Störkörper 40 mm

Die Ausbreitung des Farbstoffes nach dem Einspritzen erfolgt in radialer als auch in vertikaler Richtung. Besonders intensiv ist der Stofftransport im Bereich der Rotationsachse.

Bild 18 Umschlag bei 18/min

Bild 1 Bild 19 Zylindrische Längsstrukturen im Übergangsbereich (äußere Kugel 196 mm, innere Kugel 100 mm)

Die Zylinderstruktur, die sich an der Oberfläche der inneren Kugel befindet, ist in vertikale und horizontale Unterstrukturen aufgeteilt. Die Strukturen in der Polregion sind leider nicht deutlich zu erkennen. (Siehe auch Bild 17)

Der Störkörper ist ein Zylinder:

* Kugel 196 mm,

* Zylinderdurchmesser= Höhe = 50mm

Die Strukturen beim zylindrischen Störkörper haben große Ähnlichkeit mit den Strukturen mit kugelförmigem Störkörper. Für die Größe des Störbereiches scheint nur der Durchmesser des Störkörpers entscheidend zu sein. Das bedeutet,dass im Bereich eines in einem Fluid rotierenden Körpers ein Störbereich, ein Übergangs- und ein störfreier Bereich zu finden sind.

Bild 20 zylindrischer Störkörper, Kugel 196 mm ( Die Zahlen in den Kugeln sind Drehfrequenzen/min )

8. Duale Wellen

Alle im Kosmos vorhandenen, mit Wellen verbundene Strukturen -Kosmoswellen. folgen dem Wellengesetz:

elektromagnetische Wellen
Teilchenbewegungen in Atomen und atomaren Teilchen
Oberflächenformen auf den Planeten

Überraschend gilt das auch für die Tonfrequenzen unserer Musik (Tabelle 2).

Tabelle2 Tonfrequenzen

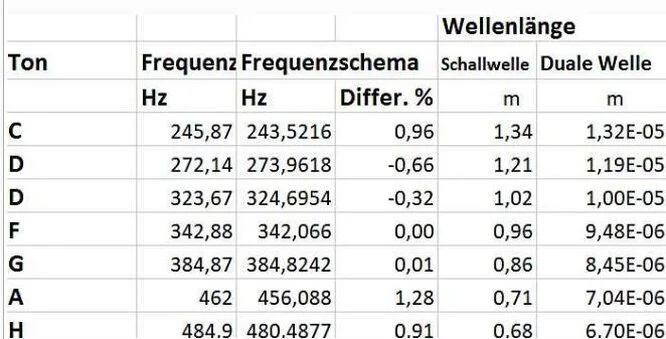
Wenn die Tonfrequenzen der Schallwellen dem Wellengesetz gehorchen, kann man mit der Wellengeschwindigkeit ("W") auch Wellenlängen berechnen, die sich von der Länge der Schallwellen unterscheiden. Ebenso gibt es für die anderen genannten Wellen einen zweiten Wert unter Verwendung der Wellengeschwindigkeit. Die Ergebnisse sind erst einmal nur reine Rechenwerte. Es ergibt sich nun die Frage, ob diese Rechenwerte einen realen Vorgang beschreiben. Das würde bedeuten, dass die Welle und ihre "duale" Welle zwei Vorgänge beschreiben, die miteinander verbunden sind. Jede Welle wäre

eine vom Medium unabhängige kosmische Welle
eine vom Medium abhängige Welle

Literatur

(1)Taylor/ G.I.; Phil. Trans.R. Soc. 1923 A 223, 289-343

(2) Witting H./ Inst. f.angew. Mathe.und Mech. ,Freiburg 1958

(3) https://photojournal.jpl.nasa.gov/

(4) Drujanow/ Rätselhafte Biographie der Erde Deutscher Verlag für Grundstoffindustrie Leipzig 1984
(5) Zürn/Schnidrig Physik Journal 1(2002) Nr.10
(6) www. .columbia.edu Photojournal
(7) R.Karsthof / Heliosseismologie, Vortrag ,PDF, Internet
(8) H.Weidner/ Hochaufgelöstese Spektrum der 0 S 3-Eigenschwingung der Erde/ Internet
(9) https://www.deepdyve.com/lp/springer-journals/die-wellenstruktur-der-singularit-ten-im- witterungsablauf- x0D4Mx6KBI
(10) Wetter 4,Satellitenfoto vom 18.1.2017,Meteogroup

Diese Webseite nutzt Cookies
OK